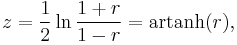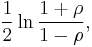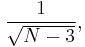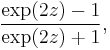Fisher transformation

In statistics, hypotheses about the value of the population correlation coefficient ρ between variables X and Y can be tested using the Fisher transformation [1][2] applied to the sample correlation coefficient r.

Contents

Definition

The transformation is defined by:

z = {1 \over 2}\ln{1%2Br \over 1-r} = \operatorname{artanh}(r),

where "ln" is the natural logarithm function and "artanh" is the inverse hyperbolic function.

If (X, Y) has a bivariate normal distribution, and if the (Xi, Yi) pairs used to form r are independent for i = 1, ..., n, then z is approximately normally distributed with mean

{1 \over 2}\ln{{1%2B\rho} \over {1-\rho}},

and standard error

{1 \over \sqrt{N-3}},

where N is the sample size.

This transformation, and its inverse,

{{\exp(2z)-1} \over {\exp(2z)%2B1}},

can be used to construct a confidence interval for ρ.

Discussion

The Fisher transformation is an approximate variance-stabilizing transformation for r when X and Y follow a bivariate normal distribution. This means that the variance of z is approximately constant for all values of the population correlation coefficient ρ. Without the Fisher transformation, the variance of r grows smaller as |ρ| gets closer to 1. Since the Fisher transformation is approximately the identity function when |r| < 1/2, it is sometimes useful to remember that the variance of r is well approximated by 1/N as long as |ρ| is not too large and N is not too small. This is related to the fact that the asymptotic variance of r is 1 for bivariate normal data.

The behavior of this transform has been extensively studied since Fisher introduced it in 1915. Fisher himself found the exact distribution of z for data from a bivariate normal distribution in 1921; Gayen, 1951[3] determined the exact distribution of z for data from a bivariate Type A Edgeworth distribution. Hotelling in 1953 calculated the Taylor series expressions for the moments of z and several related statistics[4] and Hawkins in 1989 discovered the asymptotic distribution of z for virtually any data.[5]

Other uses

While the Fisher transformation is mainly associated with the Pearson product-moment correlation coefficient for bivariate normal observations, it can also be applied to Spearman's rank correlation coefficient in more general cases. A similar result for the asymptotic distribution applies, but with a minor adjustment factor: see the latter article for details.

References

  1. ^ Fisher, R.A. (1915). "Frequency distribution of the values of the correlation coefficient in samples of an indefinitely large population". Biometrika (Biometrika Trust) 10 (4): 507–521. JSTOR 2331838. 
  2. ^ Fisher, R.A. (1921). "On the `probable error' of a coefficient of correlation deduced from a small sample". Metron 1: 3–32. http://digital.library.adelaide.edu.au/dspace/bitstream/2440/15169/1/14.pdf. 
  3. ^ Gayen, A.K. (1951). "The Frequency Distribution of the Product-Moment Correlation Coefficient in Random Samples of Any Size Drawn from Non-Normal Universes". Biometrika (Biometrika Trust) 38 (1/2): 219–247. JSTOR 2332329. 
  4. ^ Hotelling, H (1953). "New light on the correlation coefficient and its transforms". Journal of the Royal Statistical Society B (Blackwell Publishing) 15 (2): 193–225. JSTOR 2983768. 
  5. ^ Hawkins, D.L. (1989). "Using U statistics to derive the asymptotic distribution of Fisher's Z statistic". The American Statistician (American Statistical Association) 43 (4): 235–237. doi:10.2307/2685369. JSTOR 2685369.